Introduction to Numpy
Contents
Introduction to Numpy¶

NumPy stands for “Numerical Python” and it is the standard Python library used for working with arrays (i.e., vectors & matrices), linear algerba, and other numerical computations. NumPy is written in C, making NumPy arrays faster and more memory efficient than Python lists or arrays, read more: (link 1, link 2, link 3).
NumPy can be installed using conda (if not already):
conda install numpy
Knowing how to use Numpy is essential in domains such as machine learning, image analysis, and image processing.
Let’s start by importing numpy, which is commonly done as follows:
import numpy as np
NumPy Arrays¶
What are Arrays?¶
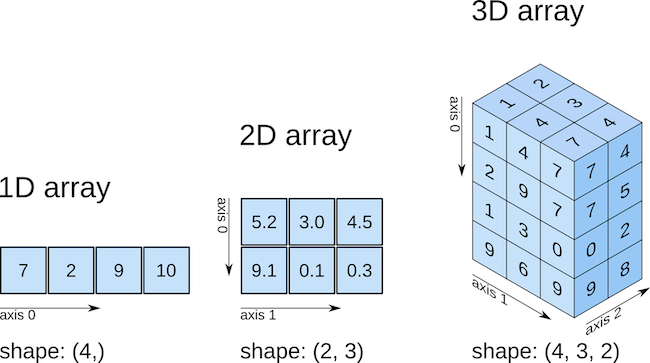
Arrays are “n-dimensional” data structures that can contain all the basic Python data types, e.g., floats, integers, strings etc, but work best with numeric data. ndarrays (which stands for n-dimensional array) are homogenous, which means that items in the array should be of the same type. ndarrays are also compatible with numpy’s vast collection of in-built functions!
Source: Medium.com
Python lists vs. numpy arrays¶
Basically, numpy arrays are a lot like Python lists. The major difference, however, is that numpy arrays may contain only a single data-type, while Python lists may contain different data-types within the same list.
Let check this out:
# Python lists may contain mixed data-types: an integer, a float, a string, a list
python_list = [1, 2.5, "whatever", [3, 4, 5]]
for value in python_list:
print(f"{str(value)} is a: {type(value)}")
1 is a: <class 'int'>
2.5 is a: <class 'float'>
whatever is a: <class 'str'>
[3, 4, 5] is a: <class 'list'>
Unlike Python lists, numpy only allows entries of the same data-type. In fact, if you try to make a numpy array with different data-types, numpy will force the entries into the same data-type (in a smart way), as is shown in the example below:
# Importantly, you often specify your arrays as Python lists first, and then convert them to numpy
to_convert_to_numpy = [1, 2, 3.5] # specify python list ...
numpy_array = np.array(to_convert_to_numpy) # ... and convert ('cast') it to numpy
for entry in numpy_array:
print(entry)
print(f'this is a: {type(entry)} \n')
1.0
this is a: <class 'numpy.float64'>
2.0
this is a: <class 'numpy.float64'>
3.5
this is a: <class 'numpy.float64'>
As you can see, Numpy converted our original list (to_convert_to_numpy), which contained both integers and floats, to an array with only floats! You might think that such a data structure that only allows one single data type is not ideal. However, the very fact that it only contains a single data-type makes operations on numpy arrays extremely fast. For example, loops over numpy arrays are often way faster than loops over python lists. This is because, internally, Python has to check the data-type of each loop entry before doing something with that entry. Because numpy arrays one allow a single data-type, it only has to check for the entries’ data type once. If you imagine looping over an array or list of length 100,000, you probably understand that the numpy loop is way faster.
Creating numpy arrays¶
As shown an earlier example, numpy arrays can be created as follows:
Define a Python list, e.g.
my_list = [0, 1, 2]Convert the list to a numpy array, e.g.
numpy_array = np.array(my_list)
Importantly, a simple Python list will be converted to a 1D numpy array, but a nested Python list will be converted to a 2D (or even higher-dimensional array). Nesting is simply combining different lists, separated by commans, as is shown here:
my_list = [1, 2, 3]
my_array = np.array(my_list)
print("A 1D (or 'flat') array:")
print(my_array, '\n')
my_nested_list = [[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]
my_2D_array = np.array(my_nested_list)
print("A 2D array:")
print(my_2D_array)
A 1D (or 'flat') array:
[1 2 3]
A 2D array:
[[1 2 3]
[4 5 6]
[7 8 9]]
and store it in a variable named vec.
# YOUR CODE HERE
Create the following matrix (2D array): math:: \begin{align} \begin{bmatrix} 5 & 2 & 8 \ 8 & 2 & 1 \ 4 & 4 & 4 \ 1 & 2 & 3 \end{bmatrix} \end{align}
and store it in a variable named arr_2d. Hint: start by creating a nested python list (like we did with the my_nested_list variable) and then convert it to numpy.
# YOUR CODE HERE
As you can imagine, creating numpy arrays from nested lists becomes cumbersome if you want to create (large) arrays with more than 2 dimensions. There are, fortunately, a lot of other ways to create (‘initialize’) large, high-dimensional numpy arrays. One often-used method is to create an array with zeros using the numpy function np.zeros. This function takes one (mandatory) argument, which is a tuple with the dimensions of your desired array:
my_desired_dimensions = (2, 5) # suppose I want to create a matrix with zeros of size 2 by 5
my_array = np.zeros(my_desired_dimensions)
print(my_array)
[[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]]
Using arrays with zeros is often used in what is called ‘pre-allocation’, in which we create an ‘empty’ array with only zeros and for example, ‘fill’ that array in a loop. Below, we can see an example where we pre-allocate an array with 5 zeros, and fill that in a for-loop with the squares of 1 - 5.
my_array = np.zeros(5)
print('Original zeros-array')
print(my_array)
for i in range(5): # notice the range function here! This loop now iterates over [0, 1, 2, 3, 4]
number_to_calculate_the_square_of = i + 1
my_array[i] = number_to_calculate_the_square_of ** 2
print('\nFilled array')
print(my_array)
Original zeros-array
[0. 0. 0. 0. 0.]
Filled array
[ 1. 4. 9. 16. 25.]
In addition to np.zeros, you can create numpy arrays using other functions, like np.ones and random from the np.random module:
ones = np.ones((5, 10)) # create an array with ones
print(ones, '\n')
rndom = np.random.random((5, 10)) # Create an array filled with random values (0 - 1 uniform)
print(rndom)
[[1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]]
[[0.26128563 0.42272127 0.39136103 0.26899306 0.74398355 0.15729989
0.20953463 0.60168266 0.67361637 0.52153336]
[0.60284964 0.21125537 0.24321607 0.88746133 0.0594551 0.14951126
0.05402739 0.26400378 0.6184847 0.42648813]
[0.79625788 0.32948868 0.57420788 0.18864782 0.19923328 0.99532862
0.82699025 0.79763984 0.94824526 0.23695406]
[0.56101251 0.41276063 0.87119635 0.50911904 0.5172619 0.96655568
0.15572032 0.25255761 0.79727359 0.286775 ]
[0.0987123 0.94499251 0.50375883 0.30695846 0.07370379 0.0434628
0.69009192 0.85096536 0.16476907 0.47678718]]
Numpy indexing¶
Indexing (extracting a single value of an array) and slicing (extracting multiple values - a subset - from an array) of numpy arrays is largely the same as with regular Python lists. Let’s check out a couple of examples of a 1D array:
my_array = np.arange(10, 21) # numpy equivalent of list(range(10, 21))
print('Full array:')
print(my_array, '\n')
Full array:
[10 11 12 13 14 15 16 17 18 19 20]
print("Index the first element:")
print(my_array[0])
Index the first element:
10
print("Index the second-to-last element:")
print(my_array[-2])
Index the second-to-last element:
19
print("Slice from 5 until (not including!) 8")
print(my_array[5:8])
Slice from 5 until (not including!) 8
[15 16 17]
print("Slice from beginning until 4")
print(my_array[:4])
Slice from beginning until 4
[10 11 12 13]
Setting values in numpy arrays works the same way as lists:
my_array = np.arange(10, 21)
my_array[0] = 10000
print(my_array)
my_array[5:7] = 0
print(my_array)
[10000 11 12 13 14 15 16 17 18 19 20]
[10000 11 12 13 14 0 0 17 18 19 20]
Multidimensional indexing¶
Often, instead of working on and indexing 1D array, we’ll work with multi-dimensional (>1D) arrays. Indexing multi-dimensional arrays is, again, quite similar to indexing and slicing list.
Like indexing Python lists, indexing multidimensional numpy arrays is done with square brackets [], in which you can put as many comma-delimited numbers as there are dimensions in your array.
For example, suppose you have a 2D array of shape \(3 \times 3\) and you want to index the value in the first row and first column. You would do this as follows:
my_array = np.zeros((3, 3)) # 3 by 3 array with zeros
indexed_value = my_array[0, 0]
print("Value of first row and first column: %.1f" % indexed_value)
Value of first row and first column: 0.0
We can also extract sub-arrays using slicing/indexing. An important construct here is that we use a single colon : to select all values from a particular dimension. For example, if we want to select all column-values (second dimension) from only the first row (first dimension), do this:
some_2d_arr[0, :]
Let’s look at an examples below:
my_array = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
print(my_array, '\n')
all_column_values_from_first_row = my_array[0, :]
print('First row')
print(all_column_values_from_first_row, '\n')
all_row_values_from_first_col = my_array[:, 0]
print('First column')
print(all_row_values_from_first_col)
[[1 2 3]
[4 5 6]
[7 8 9]]
First row
[1 2 3]
First column
[1 4 7]
Methods vs. functions¶
In the previous tutorials, we learned that, in addition to functions, 'methods' exist that are like functions of an object. We've seen examples of list methods, e.g. `my_list.append(1)`, and string methods, e.g. `my_string.replace('a', 'b')`.
Like lists and strings, numpy arrays have a lot of convenient methods that you can call (like the astype method). Again, this is just like a function, but then applied to itself. Often, numpy provides both a function and method for simple operations.
Let’s look at an example:
my_array = np.arange(10) # creates a numpy array from 0 until (excluding!) 10
print(my_array, '\n')
mean_array = np.mean(my_array)
print(f'The mean of the array is: {mean_array}')
mean_array2 = my_array.mean()
print(f'The mean of the array (computed by its corresponding method) is: {mean_array2}')
print('Is the results from the numpy function the same as '
f'the corresponding method? Answer: {str(mean_array == mean_array2)}')
[0 1 2 3 4 5 6 7 8 9]
The mean of the array is: 4.5
The mean of the array (computed by its corresponding method) is: 4.5
Is the results from the numpy function the same as the corresponding method? Answer: True
If there is both a function and a method for the operation we want to apply to the array, it really doesn’t matter what we choose! Let’s look at some more (often used) methods of numpy ndarrays:
my_array = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
std_my_array = my_array.std() # same as np.std(array)
print(f"Standard deviation of my_array: {std_my_array}", '\n')
transpose_my_array = my_array.T # same as np.transpose(array)
print(f"Transpose of my_array:\n{transpose_my_array}", '\n')
min_my_array = my_array.min() # same as np.min(array)
print(f"Minimum of my_array: {my_array.min()}", '\n')
max_my_array = my_array.max() # same as np.max(array)
print(f"Maximum of my_array: {max_my_array}", '\n')
sum_my_array = my_array.sum() # same as np.sum(array)
print(f"Sum of my_array: {sum_my_array}", '\n')
Standard deviation of my_array: 2.581988897471611
Transpose of my_array:
[[1 4 7]
[2 5 8]
[3 6 9]]
Minimum of my_array: 1
Maximum of my_array: 9
Sum of my_array: 45
Importantly, a method may or may not take arguments (input). If no arguments are given, it just looks like “object.method()”, i.e. two enclosing brackets with nothing in between. However, a method may take one or more arguments (like the my_list.append(1) method)! This argument may be named or unnamed - doesn’t matter. An example:
my_array2 = np.random.random((3, 3))
print('Original array:')
print(my_array2, '\n')
print('Use the round() method with the argument 3:')
print(my_array2.round(3), '\n')
print('Use the round() method with the named argument 5:')
print(my_array2.round(decimals=5), '\n')
Original array:
[[0.61269023 0.62004833 0.38894922]
[0.07413478 0.95840186 0.13821907]
[0.52261215 0.97264459 0.52818487]]
Use the round() method with the argument 3:
[[0.613 0.62 0.389]
[0.074 0.958 0.138]
[0.523 0.973 0.528]]
Use the round() method with the named argument 5:
[[0.61269 0.62005 0.38895]
[0.07413 0.9584 0.13822]
[0.52261 0.97264 0.52818]]
In addition to the methods listed above, you’ll probably see the following methods a lot in the code of others.
Reshaping arrays:
my_array = np.arange(10)
print(my_array.reshape((5, 2))) # reshape to desired shape
[[0 1]
[2 3]
[4 5]
[6 7]
[8 9]]
Ravel (“flatten”) an array:
temporary = my_array.reshape((5, 2))
print("Initial shape: %s" % (temporary.shape,))
print(temporary.ravel()) # unroll multi-dimensional array to single 1D array
print("Shape after ravel(): %s" % (temporary.ravel().shape,))
Initial shape: (5, 2)
[0 1 2 3 4 5 6 7 8 9]
Shape after ravel(): (10,)

